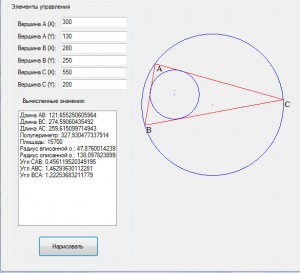
В статье мы займемся рисованием, рисовать будем треугольник, вписанную и описанную окружность. Конечно, рисовать будет программа, код которой мы сейчас напишем.
Координаты вершин треугольника будут находиться в структуре “Pt”. Для этого создадим переменные для работы со структурой и саму структуру.
Pt m1, m2, v1, v2, b1, b2;
public struct Pt
{
double x;
double y;
public Pt(double a, double b)
{
x = a;
y = b;
}
public double X
{
get { return x; }
set { x = value; }
}
public double Y
{
get { return y; }
set { y = value; }
}
};
Далее напишем функции для вычисления длин, углов треугольника и т.д. и процедуру для вывода графики на форму.
Пишем функцию нахождения длины строны треугольника по заданным координатам. Будем использовать формулу нахождения расстояния между двумя точками.
S = ((x2 - x1) ^2+ (y2-y1) ^2) ^ (1/2), где (x1, y1) и (x2, y2) - это координаты начала и конца отрезка.
double SideLength(double x1, double y1, double x2, double y2)
{
double a = Math.Sqrt((x2 - x1) / 10 * (x2 - x1) / 10 + (y2 - y1) / 10 * (y2 - y1) / 10);
return a * 10;
}
Чтобы найти углы треугольника воспользуемся формулой скалярного произведения векторов
cos(ang) = a/(s1*s2), где a - скалярное произведение векторов s1 и s2,а s1 и s2 - стороны треугольника (абсолютные величины векторов).
double Angles(Pt p1, Pt p2, Pt p3)
{
double a = (p2.X - p1.X) * (p3.X - p1.X) + (p2.Y - p1.Y) * (p3.Y - p1.Y);
double exp = a / SideLength(p1.X, p1.Y, p2.X, p2.Y) / SideLength(p1.X, p1.Y, p3.X, p3.Y);
return Math.Acos(exp);
}
Периметр находим как сумма длин трех сторон треугольника.
double Perimetr(double s1, double s2, double s3)
{
return (s1 + s2 + s3);
}
Площадь треугольника находится с помощью формулы Герона:
Sqr = (p * (p - s1) * (p - s2) * (p - s3)) ^ (1 / 2), где p - полупериметр треугольника.
double Sqare(double s1, double s2, double s3)
{
double p;
p = (Perimetr(s1, s2, s3)) / 2;
return Math.Sqrt((p * (p - s1) * (p - s2) * (p - s3)));
}
Теперь найдем радиусы вписанной и описанной окружности.
double radius(double S, double p)
{
return S / p;
}
double Radius(double S, double s1, double s2, double s3)
{
return (s1 * s2 * s3) / (4 * S);
}
И, наконец, процедура, которая будет осуществлять конечные вычисления, и рисовать окружность на форме программы.
void DescrCircle(double R, int x01, int y01, int x02, int y02, double l1, double m1, double l2, double m2)
{
double X, Y;
if ((l1 != 0) && ((m1 / l1) - (m2 / l2) != 0) && (l2 != 0))
{
X = ((m1 / l1) * x01 - y01 - (m2 / l2) * x02 + y02) / ((m1 / l1) - (m2 / l2));
Y = (m1 * X - m1 * x01 + l1 * y01) / l1;
System.Drawing.Graphics graph = this.CreateGraphics();
System.Drawing.Pen color = new Pen(Color.Blue, 1);
graph.DrawEllipse(color, (int)X, (int)Y, 1, 1); //рисуем центр окружности
graph.DrawEllipse(color, (int)X - (float)R, (int)Y - (float)R, (float)R * 2, (float)R * 2); //рисуем окружность
}
}
Процедура кнопки, которая будет вызывать всю процедуру рисования треугольника и окружностей.
private void button1_Click_1(object sender, EventArgs e)
Объявим нужные переменные и занесем в структуру координаты вершин треугольника из текстовых полей на форме.
double s1 ,s2 ,s3 ,S ,p ,r, R, ang1, ang2, ang3, x1, x2, y1, y2, det; znach.Items.Clear(); Pt[] a = new Pt[3]; a[0].X = Convert.ToDouble(Ax.Text); a[0].Y = Convert.ToDouble(Ay.Text); a[1].X = Convert.ToDouble(Bx.Text); a[1].Y = Convert.ToDouble(By.Text); a[2].X = Convert.ToDouble(Cx.Text); a[2].Y = Convert.ToDouble(Cy.Text);
Нарисуем форме три линии, которые будут составлять наш треугольник и названия вершин A, B и C.
System.Drawing.Graphics graph = this.CreateGraphics();
System.Drawing.Pen red = new Pen(Color.Red, 1);
graph.DrawLine(red, (int)a[0].X, (int)a[0].Y, (int)a[1].X, (int)a[1].Y);
graph.DrawString("A", new Font("Times New Roman", 12), new SolidBrush(Color.Black), (int)a[0].X, (int)a[0].Y);
graph.DrawLine(red, (int)a[1].X, (int)a[1].Y, (int)a[2].X, (int)a[2].Y);
graph.DrawString("B", new Font("Times New Roman", 12), new SolidBrush(Color.Black), (int)a[1].X, (int)a[1].Y);
graph.DrawLine(red, (int)a[0].X, (int)a[0].Y, (int)a[2].X, (int)a[2].Y);
graph.DrawString("C", new Font("Times New Roman", 12), new SolidBrush(Color.Black), (int)a[2].X, (int)a[2].Y);
Используя написанные функции, найдем длины сторон, полупериметр, площадь, радиусы вписанной и описанной окружности и углы треугольника.
s1 = SideLength(a[0].X, a[0].Y, a[1].X, a[1].Y); s2 = SideLength(a[1].X, a[1].Y, a[2].X, a[2].Y); s3 = SideLength(a[2].X, a[2].Y, a[0].X, a[0].Y); p = (Perimetr(s1, s2, s3)) / 2; S = Sqare(s1, s2, s3); r = radius(S, p); R = Radius(S, s1, s2, s3); ang1 = Angles(a[2], a[0], a[1]); ang2 = Angles(a[0], a[1], a[2]); ang3 = Angles(a[1], a[2], a[0]);
Выведем на форму все эти вычисленные значения в ListBox “znach”.
znach.Items.Add("Длина AB: " + s1);
znach.Items.Add("Длина BC: " + s2);
znach.Items.Add("Длина AC: " + s3);
znach.Items.Add("Полупериметр: " + p);
znach.Items.Add("Площадь: " + S);
znach.Items.Add("Радиус вписанной о.: " + r);
znach.Items.Add("Радиус описанной о.: " + R);
znach.Items.Add("Угл CAB: " + ang1);
znach.Items.Add("Угл ABC: " + ang2);
znach.Items.Add("Угл BCA: " + ang3);
Найдем середины сторон s1 и s2.
m1.X = (a[0].X + a[1].X) / 2; m1.Y = (a[0].Y + a[1].Y) / 2; m2.X = (a[1].X + a[2].X) / 2; m2.Y = (a[1].Y + a[2].Y) / 2;
Необходимо повернуть точки на угол 90 градусов.
Поворачиваем точку а[2] вокруг середины стороны:
x1 = a[2].X; y1 = a[2].Y; x1 -= m2.X; y1 -= m2.Y; b1.X = x1 * Math.Cos(Math.PI / 2) - y1 * Math.Sin(Math.PI / 2); b1.Y = x1 * Math.Sin(Math.PI / 2) + y1 * Math.Cos(Math.PI / 2); b1.X += m2.X; b1.Y += m2.Y; v1.X = b1.X - m2.X; v1.Y = b1.Y - m2.Y;
Поворачиваем точку а[0] вокруг середины стороны s1:
x1 = a[0].X; y1 = a[0].Y; x1 -= m1.X; y1 -= m1.Y; b2.X = x1 * Math.Cos(Math.PI / 2) - y1 * Math.Sin(Math.PI / 2); b2.Y = x1 * Math.Sin(Math.PI / 2) + y1 * Math.Cos(Math.PI / 2); b2.X += m1.X; b2.Y += m1.Y; v2.X = b2.X - m1.X; v2.Y = b2.Y - m1.Y;
Вызовем нашу процедуру для вывода графики и построим описанную окружность с центром в точке пересечения серединных перепендикуляров.
DescrCircle(R, (int)m1.X, (int)m1.Y, (int)m2.X, (int)m2.Y, v2.X, v2.Y, v1.X, v1.Y);
int coef1 = 1, coef2 = 1; //коэффициенты,указывающие напрвление поворота
Вычисляем знак третьей координаты векторного произведения векторов, между которыми строится биссектриса.
det = (a[1].X - a[0].X) * (a[2].Y - a[0].Y) - (a[2].X - a[0].X) * (a[1].Y - a[0].Y); if (det > 0) coef1 = -1; det = (a[1].X - a[2].X) * (a[0].Y - a[2].Y) - (a[0].X - a[2].X) * (a[1].Y - a[2].Y); if (det > 0) coef2 = -1;
Поворачиваем точку a[2] вокруг a[0] на угол равный половине угла ang2
x1 = a[2].X; y1 = a[2].Y; x1 -= a[0].X; y1 -= a[0].Y; b1.X = x1 * Math.Cos(coef1 * ang2 / 2) - y1 * Math.Sin(coef1 * ang2 / 2); b1.Y = x1 * Math.Sin(coef1 * ang2 / 2) + y1 * Math.Cos(coef1 * ang2 / 2); b1.X += a[0].X; b1.Y += a[0].Y; v1.X = b1.X - a[0].X; v1.Y = b1.Y - a[0].Y; x2 = a[0].X; y2 = a[0].Y; x2 -= a[2].X; y2 -= a[2].Y; b2.X = x2 * Math.Cos(coef2 * ang1 / 2) - y2 * Math.Sin(coef2 * ang1 / 2); b2.Y = x2 * Math.Sin(coef2 * ang1 / 2) + y2 * Math.Cos(coef2 * ang1 / 2); b2.X += a[2].X; b2.Y += a[2].Y; v2.X = b2.X - a[2].X; v2.Y = b2.Y - a[2].Y; //v1.x v1.y- координаты направляющего вектора биссектрисы
И последнее, что мы делаем это выполняем построение вписанной окружности с центром в точке пересечения биссектрисс.
DescrCircle(r, (int)a[2].X, (int)a[2].Y, (int)a[0].X, (int)a[0].Y, v2.X, v2.Y, v1.X, v1.Y);
Треугольник и две окружности построены, для решения этой задачи нам понадобились небольшие знания C# и геометрии.
Автор: Евтеев Евгений Александрович