В предшествующей статье я рассказал, как найти наибольшее общее кратное двух чисел, используя алгоритм вычисления НОД. В этой статей мы с вами напишем универсальный алгоритм нахождения НОК. Этот алгоритм позволяет найти НОК не только для двух чисел, но для множества чисел.
Наименьшее общее кратное
Начнем с создания формы проекта, примерная форма показана на рисунке:
Наименьшее общее кратное
Форму создали, разместили необходимые объекты на ней. Теперь будем заниматься написанием кода программы. Числа, для которых будет производиться поиск наименьшее общее кратное (НОК), будут вводиться через пробел. Для того, что их читать из поля “n_gr ” напишем функцию.
string[] nums(string str, int f_m) {
string[] numbers = new string[f_m + 1];
f_m = 0;
for (int i = 0; i < str.Length; i++) {
if (str.Substring(i, 1) != " ")
numbers[f_m] += str.Substring(i, 1);
else
f_m++;
}
return numbers;
}
Входные параметры “str” и “f_m” – это строка с числа и количество чисел соответственно. Создаем массив размерностью “f_m” и начинаем “выдирать” числа из строки и добавлять их в массив “numbers”. Функция возращает массив с числами из строки.
Теперь процедура события клика по кнопке “find”:
private void find_Click(object sender, EventArgs e) {
string s = n_gr.Text;
int i = 0, f_m = 0;
while (i < s.Length) {
if (s.Substring(i, 1) == " ")
f_m++;
i++;
}
string[] numbers = new string[f_m + 1];
numbers = nums(s, f_m);
int c = 2;
bool nok = true;
for (; ; ) {
for (i = 0; i < numbers.Length; i++)
if (numbers[i] != "")
if (c % Convert.ToInt32(numbers[i]) == 0) {
if (i == 0 || nok == true)
nok = true;
}
else
nok = false;
if (nok == true) {
n_nok2.Text = Convert.ToString(c);
break;
}
if (c >= 1000000) {
n_nok2.Text = "НОК для данных чисел не найден!";
break;
}
c++;
}
}
Здесь сначала вычисляется количество чисел в введенной строке, создается и заполняется массив с числами. Затем используется следующий алгоритм вычисления НОК: постоянно увеличивающееся число 2 делим на каждое из введенных чисел и НОК будет найден в том случае, когда остаток от деления на каждое число будет равен нулю. Если НОК найден или количество проходов цикла перевалило за 1000000 прекращаем работу программы, выводим соответствующий результат ее работы.
Универсальный алгоритм вычисления наименьшее общее кратное
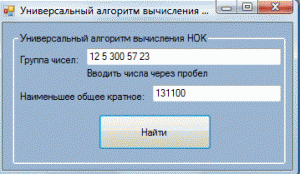
На рисунке показан пример удачного поиска НОК, универсальный алгоритм работает правильно.
Автор: Евтеев Евгений Александрович
